Rumus Persegi Panjang: Bentuk, Ciri-Ciri, Luas, Keliling

Rumus Persegi Panjang: Bentuk, Ciri-Ciri, Luas, Keliling | Info Vuiral – Pembahasan lengkap mengenai pelajaran matematika tentang bentuk, ciri-ciri, rumus luas dan keliling yang terdapat pada bangun datar persegi panjang dan disertai contoh soalnya.

Baca juga: Kumpulan Simbol Matematika Bangun Datar Dan Bangun Ruang

Rumus Persegi Panjang: Pengertian, Bentuk, Ciri-Ciri, Menghitung Luas, Keliling, Diagonal

Pengertian Persegi Panjang

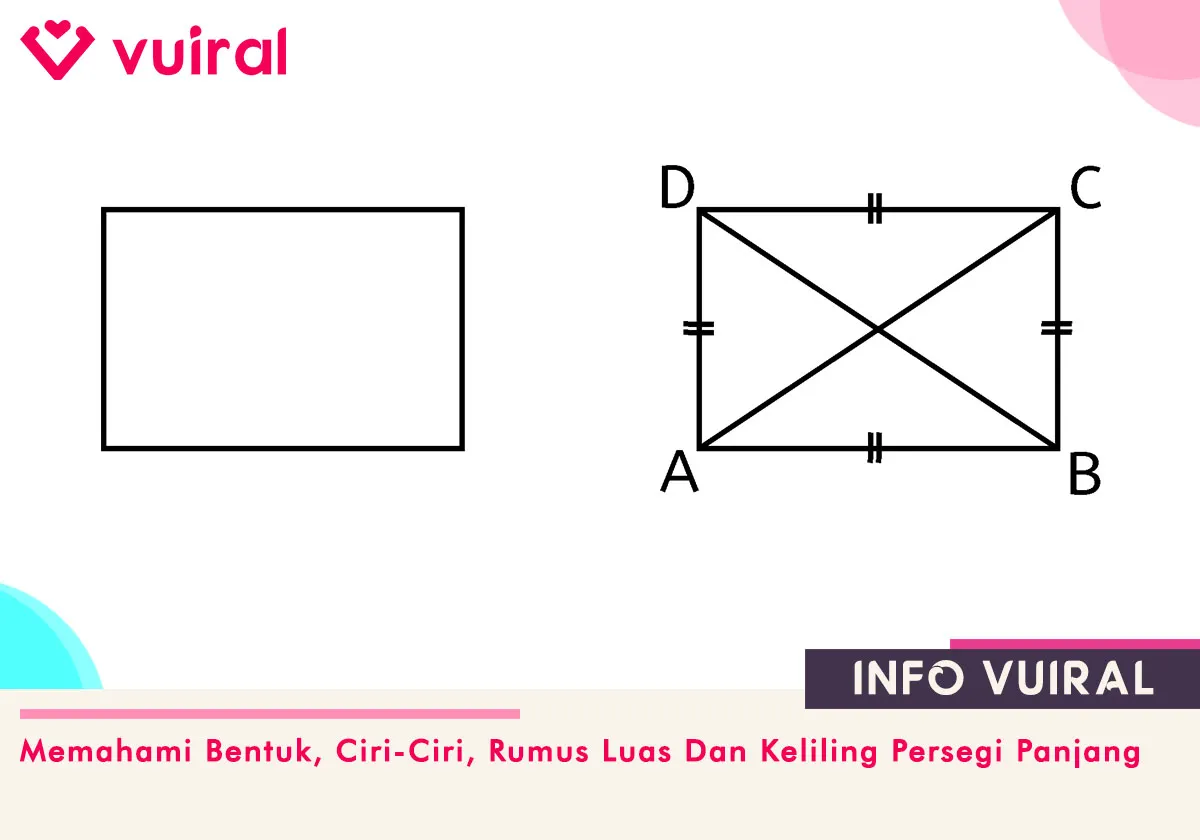
Persegi Panjang adalah bangun datar dua dimensi yang memiliki 2 pasang sisi berhadapan yang sama panjang serta memiliki 4 sudut siku-siku 90°.

Contoh Gambar Bentuk Persegi Panjang

Gambar Bentuk Persegi Panjang

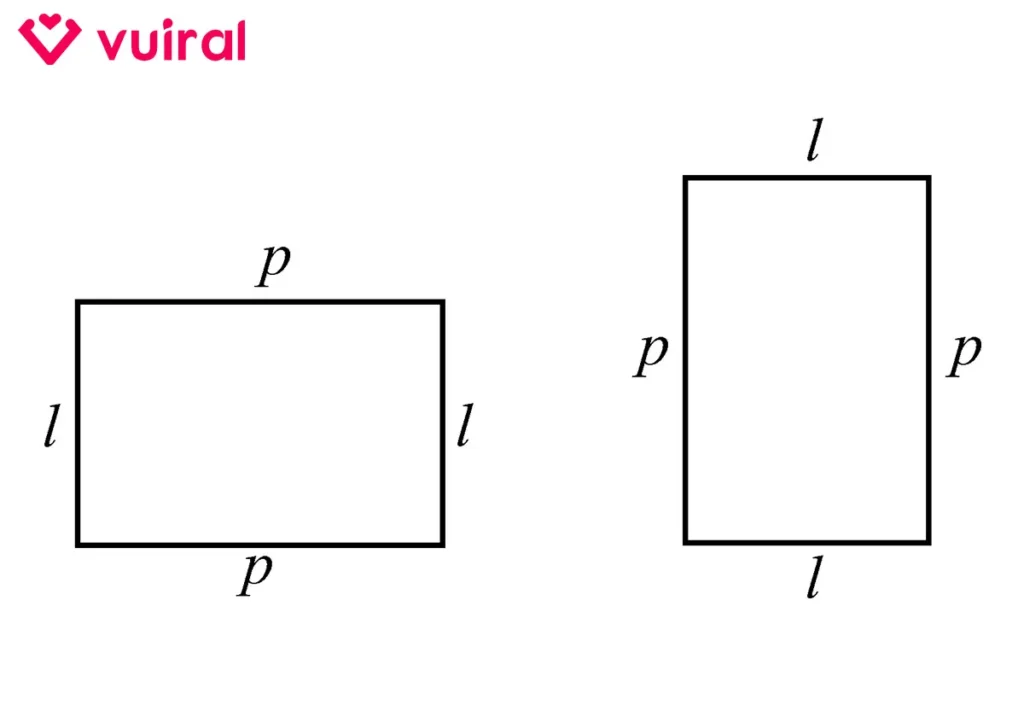
Contoh letak Panjang (p) dan Lebar (l) pada bangun datar persegi panjang. Lokasi panjang dan lebar disesuaikan dengan ukuran bangun datar tersebut meskipun dilihat dari sudut pandang manapun.

Gambar Bentuk Persegi Panjang Dengan Letak Sudut Dan Diagonal

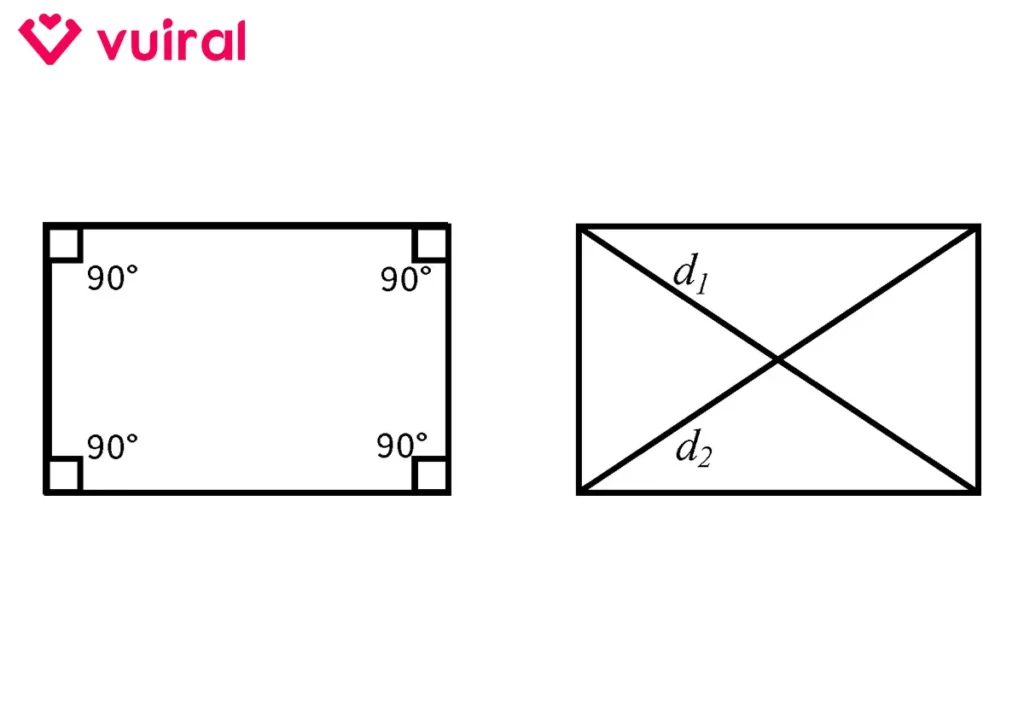
Contoh besar sudut dan letak diagonal pada bangun datar persegi panjang.

Ciri-Ciri Atau Sifat-Sifat Persegi Panjang

• Memiliki 4 sisi, dan sisi-sisinya yang berhadapan sama panjang (AB=CD dan AD=BC).
• Mempunyai 2 pasang sisi yang sejajar (AB // CD dan AD // BC).
• Memiliki 4 sudut siku-siku 90° (∠A; ∠B; ∠C; ∠D).
• Memiliki 2 diagonal yang berpotongan dan mempunyai panjang yang sama (AC dan BD).
• Mempunyai 2 simetri lipat (DA→BC dan DC→AB)
• Mempunyai 2 simetri putar (A→C B→D dan A→A B→B)

Baca juga: Rumus Persegi (Bujur Sangkar): Pengertian, Bentuk, Ciri-Ciri, Luas, Keliling

Rumus Bangun Datar Persegi Panjang: Menghitung Luas, Keliling, Diagonal, Panjang Dan Lebar

Rumus Luas Persegi Panjang
Rumus untuk mencari Luas (L) persegi panjang adalah Panjang (p) × Lebar (l), seperti rumus berikut:

Luas (L) = p × l

Rumus mencari diagonal pada bangun datar Persegi Panjang
Untuk mencari panjang diagonal pada bangun datar persegi panjang maka kalian harus menggunakan rumus berikut.

Diagonal (d) = √ (p² + l²)

Rumus Keliling Persegi Panjang
Sedangkan rumus untuk mencari Keliling (K) persegi panjang adalah Panjang (p) + Panjang (p) + Lebar (l) + Lebar (l), seperti rumus berikut.

Keliling (K) = p + p + l + l atau 2 × (p + l)

Rumus mencari Panjang pada bangun datar Persegi Panjang
Mencari Panjang persegi panjang jika mengetahui dari Luas dan Lebar.

Panjang (p) = L ÷ l

Mencari Panjang persegi panjang jika diketahui dari Keliling dan Lebar.

Panjang (p) = (K ÷ 2) – l

Rumus mencari Lebar pada bangun datar Persegi Panjang
Mencari Lebar persegi panjang jika mengetahui dari Luas dan Panjang.

Lebar (l) = L ÷ p

Mencari Lebar persegi panjang jika diketahui dari Keliling dan Panjang.

Lebar (l) = (K ÷ 2) – p

Contoh Soal Matematika Tentang Bangun Datar Persegi Panjang

1. Diketahui sebuah persegi panjang memiliki panjang 15 cm dan lebar 7 cm. Tentukan Luas (L) dan Keliling (K) dari persegi panjang tersebut!

Jawaban:
Gunakan rumus untuk mencari luas persegi panjang.
L = p × l = 15 × 7 = 105 cm².

Gunakan rumus untuk mencari keliling persegi panjang.
K = 2 × (p + l) = 2 × (15 + 7) = 2 × (22) = 44 cm.

2. Ada sebuah bangun datar dengan bentuk persegi panjang, jika diketahui lebarnya 8 cm dan luasnya 96 cm². Meka berapakah Panjang (p) dari bangun datar tersebut?

Jawaban:
p = L ÷ l = 96 ÷ 8 = 12 cm.

3. Terdapat sebuah bangun datar berbentuk persegi panjang yang memiliki panjang 25 cm dengan keliling 74 cm. Carilah Lebar (l) pada bangun datar tersebut!

Jawaban:
p = (K ÷ 2) – p =(74 ÷ 2) – 25 = 37 – 25 = 12 cm.

4. Diketahui sebuah keliling persegi panjang yaitu 144 cm dengan lebar 27 cm. Berapakah Diagonal (d) dari persegi panjang tersebut?

Jawaban:
Gunakan rumus untuk mencari Panjang dari persegi panjang tersebut.
p = (K ÷ 2) – p =(144 ÷ 2) – 27 = 72 – 27 = 45 cm.

Kemudian setelah kita mengetahui panjang dan lebar dari persegi panjang tersebut, barulah kita bisa mencari diagonalnya.
d = √ (p² + l²) = √ 45² + 27² = √ 2025 + 729 = √2754 = 52,48 cm.

Itulah pembahasan lengkap mengenai pelajaran matematika tentang bentuk, ciri-ciri, rumus luas dan keliling yang terdapat pada bangun datar persegi panjang dan disertai contoh soalnya yang dapat kalian pelajari. Semoga artikel ini dapat membantu kalian untuk menyelesaikan soal matematika tersebut.