Bentuk, Ciri-Ciri, Rumus Luas Dan Keliling Trapesium (Lengkap)
Bentuk, Ciri-Ciri, Rumus Luas Dan Keliling Trapesium (Lengkap) | Info Vuiral – Pembahasan lengkap mengenai pelajaran matematika tentang bentuk, ciri-ciri, rumus luas dan keliling yang terdapat pada bangun datar trapesium dan disertai contoh soalnya dengan jawabannya.
Pengertian, Bentuk, Ciri-Ciri, Menghitung Rumus Luas Dan Keliling Trapesium Beserta Mencari Alas Dan Tinggi Segitiga
Pengertian Trapesium
Trapesium adalah sebuah bangun datar yang dibentuk oleh 4 ruas dan 2 ruas diantaranya saling sejajar namun tidak sama panjang, selain itu trapesium memiliki 1 atau 2 titik sudut tumpul.
Baca juga: Rumus Layang-Layang: Luas, Keliling, Bentuk, Ciri-Ciri
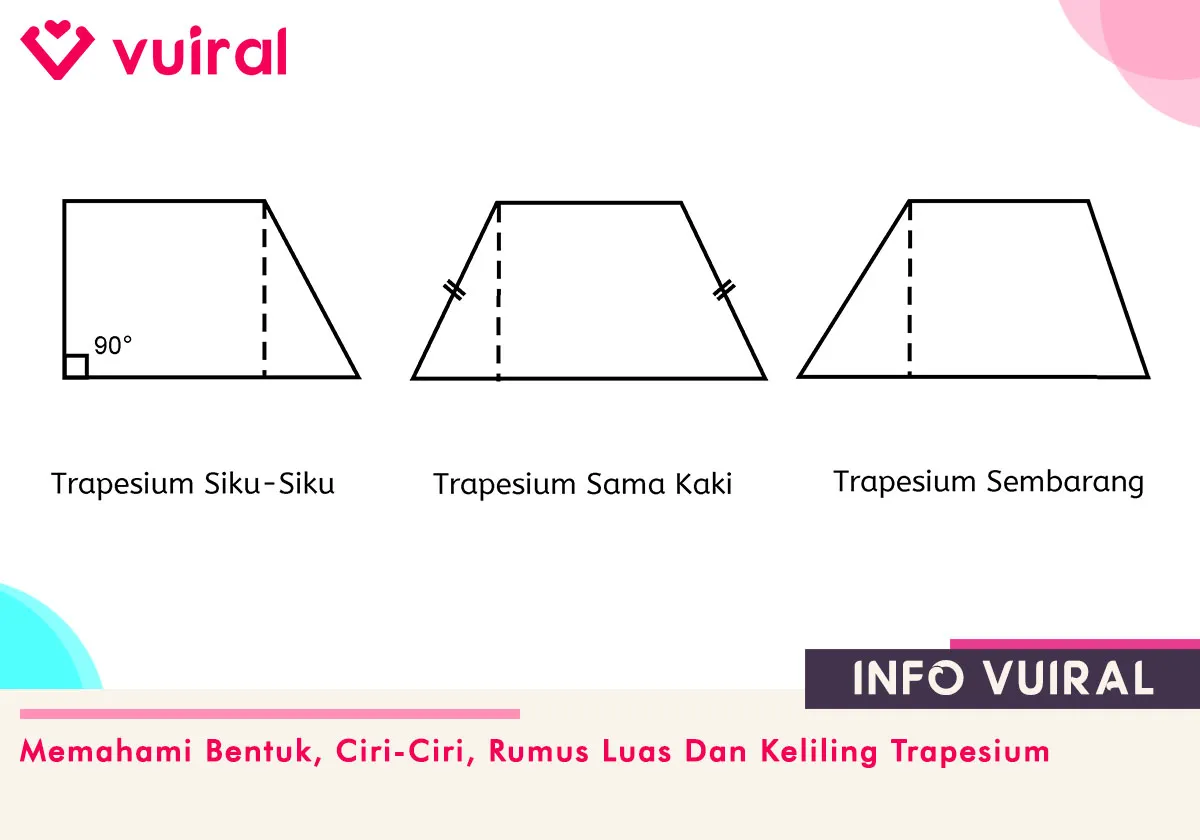
Contoh Gambar Bentuk-Bentuk Trapesium
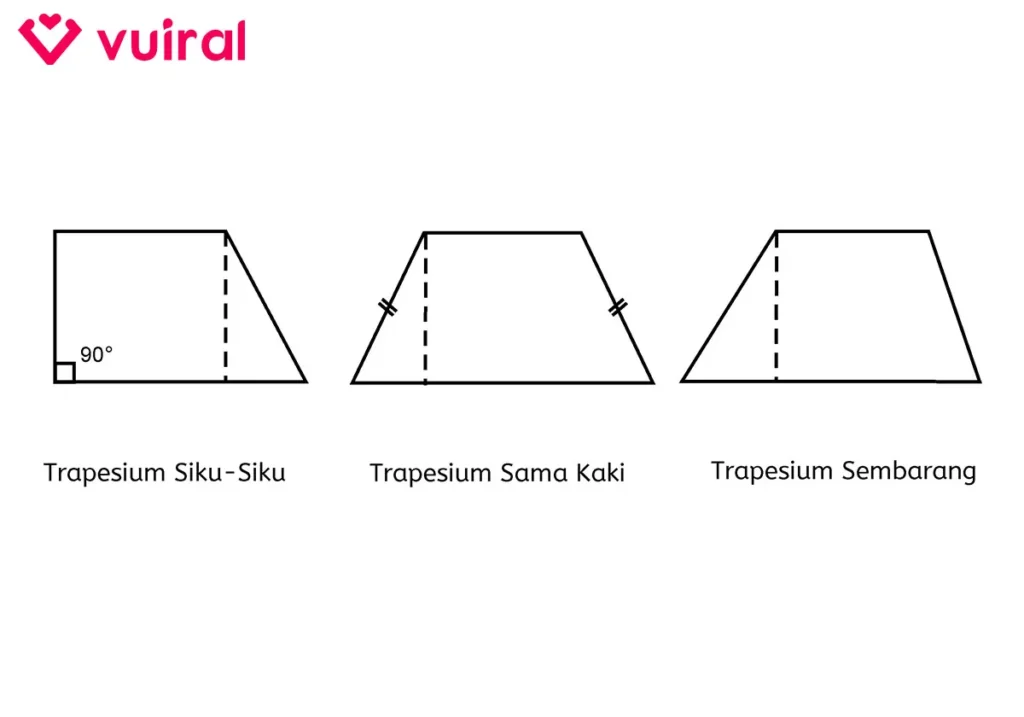
- Trapesium Siku-siku
Trapesium Siku-Siku memiliki 1 titik sudut tumpul dan 2 titik sudut yang membentuk siku-siku 90°. - Trapesium Sama Kaki
Trapesium Sama Kaki merupakan sebuah bentuk trapesium dengan 1 pasang sisi tidak sejajar yang sama panjang. - Trapesium Sembarang
Trapesium Sembarang adalah sebuah bangun trapesium dengan semua ukuran panjang sisinya dan besar sudutnya berbeda.
Ciri-Ciri Atau Sifat-Sifat Trapesium
- Memiliki sepasang sisi sejajar yang tidak sama panjang (AB // CD).
- Memiliki 4 titik sudut (∠A + ∠B + ∠C + ∠D = 360°).
- Mempunyai 1 simetri lipat (khusus untuk Trapesium Sama Kaki).
- Mempunyai 1 simetri putar.
- Minimal memiliki satu titik sudut tumpul.
Baca juga: Bentuk, Ciri-Ciri, Rumus Luas Dan Keliling Segitiga (Lengkap)
Rumus Untuk Mencari Luas, Keliling, Alas Dan Tinggi Pada Trapesium
Rumus Luas Trapesium
Luas (L) = ½ × t × (AB + CD)
Rumus Keliling Trapesium
Keliling (K) = AB + BC + CD + DA
Rumus Mencari Tinggi Trapesium Siku-Siku
Tinggi (t) = √BC² – (AB – CD)²
Rumus Mencari Sisi Alas Trapesium Siku-Siku
Sisi AB = CD + √BC² – t²
Rumus Mencari Sisi Miring Trapesium Siku-Siku
Sisi BC = √t² – (AB – CD)²
Rumus Keliling Trapesium Sama Kaki
Keliling (K) = AB + CD + (2 × Sisi miring BC atau DA)
Rumus Mencari Tinggi Trapesium Sama Kaki
Tinggi (t)= √(BC² – ((AB – CD) ÷ 2)²)
Rumus Mencari Sisi Sejajar Trapesium Sama Kaki
Sisi AB = CD + √(BC² – t²)
Sisi CD = AB – √(BC² – t²)
Rumus Mencari Sisi Miring Trapesium Sama Kaki
Sisi BC = DA = (K – AB – CD) ÷ 2
*sebenarnya ukuran sisi miring BC=DA begitu pula sebaliknya
Rumus Mencari Tinggi Trapesium Sembarang
Tinggi (t) = 2 × L ÷ (AB + CD)
Rumus Mencari Sisi Sejajar Trapesium Sembarang
Sisi AB = K – CD – BC – DA
Sisi CD = K – AB – BC – DA
Rumus Mencari Sisi Miring Trapesium Sembarang
Sisi BC = K – AB – CD – DA
Sisi DA = K – AB – BC – CD
Baca juga: Rumus Belah Ketupat: Bentuk, Ciri-Ciri, Luas, Keliling
Contoh Soal Tentang Bangun Datar Trapesium
- Diketahui sebuah bangun trapesium dengan sisi sejajar (AB = 16 cm) dan (CD = 10 cm), sedangkan sisi miringnya adalah (BC = 10 cm) dan (DA = ?) serta tingginya 8 cm. Hitunglah luas trapesium tersebut!
Jawaban:
Untuk mencari luas, pakailah rumus mencari luas trapesium.
Luas (L) = ½ × t × (AB + CD)
L = ½ × 8 × (16 + 10)
L = ½ × 8 × 26
L = 104 cm²
- Diketahui panjang sisi sejajar trapesium tersebut (AB = 13 cm) dan (CD = 8 cm), serta salah satu sisi miringnya adalah (BC = 7 cm) dan (DA = 5 cm). Hitunglah berapa keliling trapesium tersebut!
Jawaban:
Untuk mencari luas, pakailah rumus mencari keliling trapesium.
Keliling (K) = AB + BC + CD + DA
K = 13 + 7 + 8 + 5
K = 33 cm
- Sebuah trapesium sama kaki dengan sisi sejajar sepanjang (AB = 16 cm) dan (CD = 10 cm), lalu memiliki sisi miringnya ialah (BC = 10 cm). Maka carilah tinggi dari trapesium sama kaki tersebut!
Jawaban:
Untuk mencari tingginya, gunakan rumus mencari tinggi trapesium sama kaki.
Tinggi (t) = √(BC² – ((AB – CD) ÷ 2)²)
t = √(10² – ((16 – 10) ÷ 2)²)
t = √(10² – (6 ÷ 2)²)
t = √(10² – 3²)
t = √(100 – 9)
t = √91
t = 9,54 cm
Itulah pembahasan lengkap mengenai pelajaran matematika tentang bentuk, ciri-ciri, rumus luas dan keliling yang terdapat pada bangun datar trapesium dan disertai contoh soalnya yang bisa kalian pelajari sendiri. Semoga artikel ini dapat membantu kalian untuk menyelesaikan soal matematika kamu.