Contoh Soal Volume Dan Luas Permukaan Tabung Beserta Jawabannya
Contoh Soal Volume Dan Luas Permukaan Tabung Beserta Jawabannya | Info Vuiral – Pembahasan lengkap mengenai pelajaran matematika tentang rumus volume tabung dan luas permukaan tabung yang disertai dengan contoh soalnya.
Contoh Latihan Soal Matematika: Rumus Volume Dan Luas Permukaan Pada Bangun Ruang Tabung Beserta Jawabannya
Pengertian Bangun Ruang Tabung
Tabung adalah bangun ruang sisi lengkung dalam bentuk 3 dimensi yang memiliki 2 bidang berbentuk lingkaran sebagai sisi alasnya dan 1 bidang lengkung sebagai sisi tegak yang bisa disebut dengan nama selimut tabung.
Tabung juga bisa disebut dengan prisma segi nol (0) karena tabung juga mempunyai sifat-sifat yang dimiliki bangun ruang prisma, yaitu memiliki 2 alas dan sisi bidang tegak di bagian sampingnya.
Baca juga: Contoh Soal Volume Dan Luas Permukaan Limas Beserta Jawabannya
Contoh Gambar Bentuk Bangun Ruang Tabung Dan Keterangannya
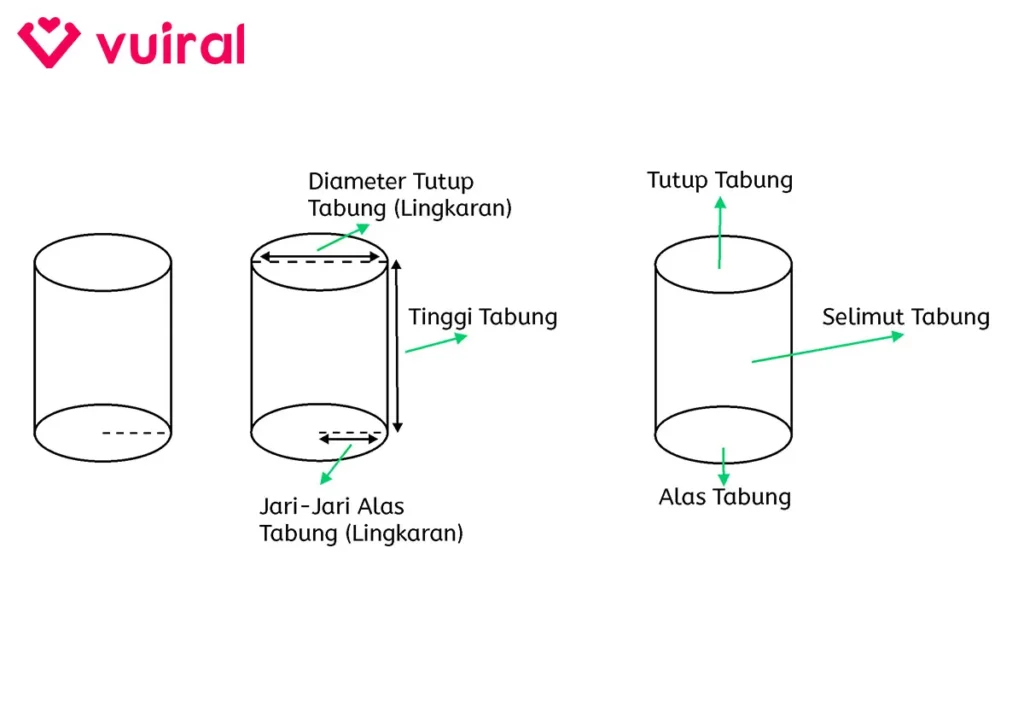
Keterangan:
- Diameter Tabung ialah panjang ukuran satu lingkaran penuh dari tabung.
- Jari-Jari Tabung ialah panjang ukuran setengah lingkaran tabung.
- Tinggi Tabung ialah tinggi dari titik ujung alas hingga titik ujung tutup pada tabung.
- Tutup Tabung adalah bidang alas bagian atas tabung.
- Alas Tabung adalah bidang alas bagian bawah tabung.
- Selimut tabung adalah bidang lengkung yang menyelimuti bagian samping tabung.
Cara Menghitung Rumus Volume, Luas Permukaan Dan Tinggi Tabung
Cara Menghitung Rumus Volume Tabung
V = Luas alas Tabung × tinggi Tabung
V = π × r × r × t
Cara Menghitung Rumus Luas Permukaan Tabung
LP = 2 × La Tabung + Ls Tabung
LP = 2 × π × r × r + 2 × π × r × t
atau
LP = 2 × π × r × (r + t)
a. Rumus Luas Permukaan Tabung Tanpa Alas Atau Tutup
LP = La Tabung + Ls Tabung
LP = π × r × r + 2 × π × r × t
b. Rumus Luas Selimut Tabung (Sisi Lengkung / Persegi)
Ls = 2 × π × r × t
c. Rumus Luas Alas Atau Tutup Tabung (Lingkaran)
La = π × r × r
atau
La = π × r²
Cara Menghitung Rumus Diameter Alas Lingkaran Pada Tabung
a. Jika Diketahui Jari-Jari Lingkaran
d = r + r
atau
d = 2 × r
b. Jika Diketahui Keliling Lingkaran
d = K ÷ (2 × π) × 2
c. Jika Diketahui Luas Lingkaran
d = (K × 7/22) ÷ 2
Cara Menghitung Rumus Jari-Jari Alas Lingkaran Pada Tabung
a. Jika Diketahui Diameter Lingkaran
r = d ÷ 2
b. Jika Diketahui Keliling Lingkaran
r = K ÷ (2 × π)
c. Jika Diketahui Luas Lingkaran
r = √(L × 7/22)
Cara Menghitung Rumus Tinggi Selimut Tabung
a. Jika Diketahui Volume Tabung Dan Jari-Jari
t = V ÷ (π × r × r)
b. Jika Diketahui Volume Tabung Dan Luas Alas Atau Tutup Tabung
t = V ÷ La Tabung
c. Jika Diketahui Luas Permukaan Dan Jari-Jari
t = (LP – 2 × La) ÷ 2 × π × r
Keterangan:
- V = Volume Tabung
- LP = Luas Permukaan Tabung
- Ls = Luas selimut Tabung
- La = Luas alas Tabung
- π (pi) = 22/7 atau 3,14 (dipakai untuk rumus lingkaran)
- r (radius) = Jari-Jari lingkaran Tabung
- d = Diameter lingkaran Tabung
- t = Tinggi Tabung
Baca juga: Contoh Soal Volume Dan Luas Permukaan Prisma Beserta Jawabannya
Contoh Soal Volume Dan Luas Permukaan Tabung Beserta Jawabannya
Soal Nomor 1
Hitunglah volume bangun ruang tabung dengan diameter 14 cm dan tinggi tabung 30 cm!
Jawaban:
Menghitung jari-jari tabung
r = d ÷ 2
r = 14 ÷ 2
r = 7 cm
Menghitung volume tabung
V = Luas alas Tabung × tinggi Tabung
V = π × r × r × t
V = 22/7 × 7 × 7 × 30
V = 4.620 cm³
Soal Nomor 2
Hitunglah luas permukaan bangun ruang tabung jika diketahui jari-jarinya sepanjang 14 cm dan tinggi tabung 40 cm!
Jawaban:
Menghitung luas permukaan tabung
LP = 2 × La Tabung + Ls Tabung
LP = 2 × π × r × r + 2 × π × r × t
LP = 2 × 22/7 × 14 × 14 + 2 × 22/7 × 14 × 40
LP = 1232 + 3520
LP = 4.752 cm²
Soal Nomor 3
Apabila sebuah tabung memiliki jari-jari sepanjang 28 cm dan tinggi 60 cm. Maka berapakah luas permukaan tabung tersebut jika tanpa penutupnya?
Jawaban:
LP = La Tabung + Ls Tabung
LP = π × r × r + 2 × π × r × t
LP = 22/7 × 28 × 28 + 2 × 22/7 × 28 × 60
LP = 2464 + 10560
LP = 13.024 cm²
Baca juga: Bangun Ruang Bola: Pengertian, Bentuk, Ciri-Ciri, Rumus
Soal Nomor 4
Carilah luas selimut tabung dengan diameter 10 cm dan tinggi tabung 20 cm!
Jawaban:
Menghitung jari-jari tabung
r = d ÷ 2
r = 10 ÷ 2
r = 5 cm
Menghitung luas selimut tabung
Ls = 2 × π × r × t
Ls = 2 × 3,14 × 5 × 20
Ls = 628 cm²
Soal Nomor 5
Sebuah tabung memiliki volume 3.080 cm³ dan jari jari tabung tersebut ialah 7 cm. Bagaimana cara untuk mengetahui tinggi tabung?
Jawaban:
Menghitung tinggi tabung jika diketahui volume dan jari-jari
t = V ÷ (π × r × r)
t = 3080 ÷ (22/7 × 7 × 7)
t = 3080 ÷ 154
t = 20 cm
Soal Nomor 6
Jika diketahui bangun ruang tabung memiliki luas permukaan sebesar 1.188 cm² dan jari-jari sepanjang 7 cm. Maka tinggi tabung tersebut berapa cm?
Jawaban:
Menghitung luas alas tabung untuk mengetahui tinggi tabung
La = π × r × r
La = 22/7 × 7 × 7
La = 154 cm²
Menghitung tinggi tabung jika diketahui luas permukaan dan luas alas
t = (LP – 2 × La) ÷ 2 × π × r
t = (1188 – 2 × 154) ÷ 2 × 22/7 × 7
t = (1188 – 308) ÷ 44
t = 880 ÷ 44
t = 20 cm²
Itulah artikel mengenai contoh latihan soal matematika: rumus volume dan luas permukaan pada bangun ruang tabung beserta jawabannya, yap meskipun pembahasannya sangat panjang tapi saya sudah berusaha untuk menyederhanakannya supaya lebih mudah dipahami dan semoga saja bisa bermanfaat ya teman-teman.